目次
[音楽的話]音楽的調和を深堀する
ダイアトニックスケールという調和の可視化
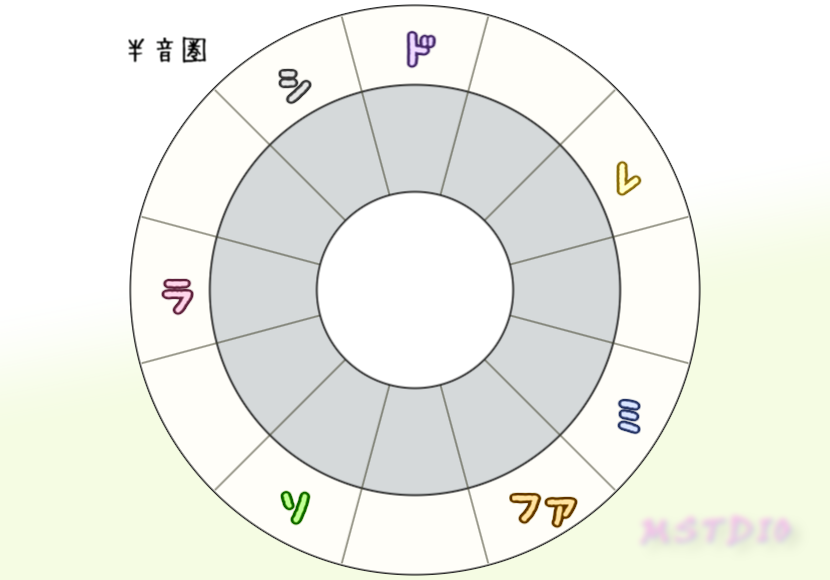
メジャースケールがこの2つの距離でどうなっているか見てみよう。簡単に考えるためにCメジャースケールを考えてみるよ。
前回までの記事はこちら
おさらいを踏まえておこう
- 半音圏上近い音は、メロディック(旋律的)。音高の落差が少ないので時間差で鳴らすと穏やかだが、同時に鳴らすと濁りやすい
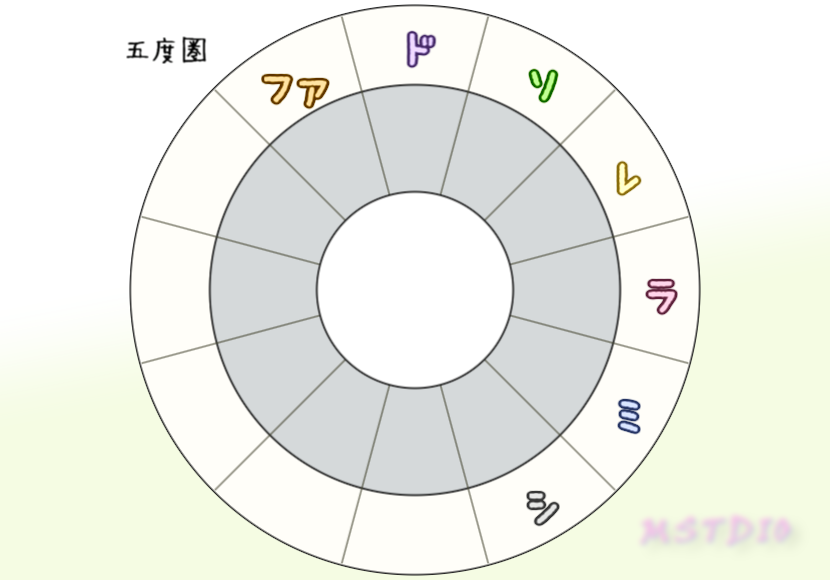
- 五度圏上近い音は、ハーモニック(和声的)。音高の落差が多いので時間差で鳴らすと激しくインパクトがあるが、同時に鳴らすと調和しやすい
半音圏でメロディックな考察、五度圏ではハーモニックな考察ができそうだね
スケール(和声的)としての調和
可視化するとぱっと見でもハーモニー的に素晴らしく調和のとれたスケールなんだなってわかる。五度圏(近いほど調和)の密集具合をみると、隙間が開いてない密着した近所の音たちだってことがわかるし、半音圏(離れるほど調和)の離散具合からもそれがわかる。
スケール(旋律的)としての調和
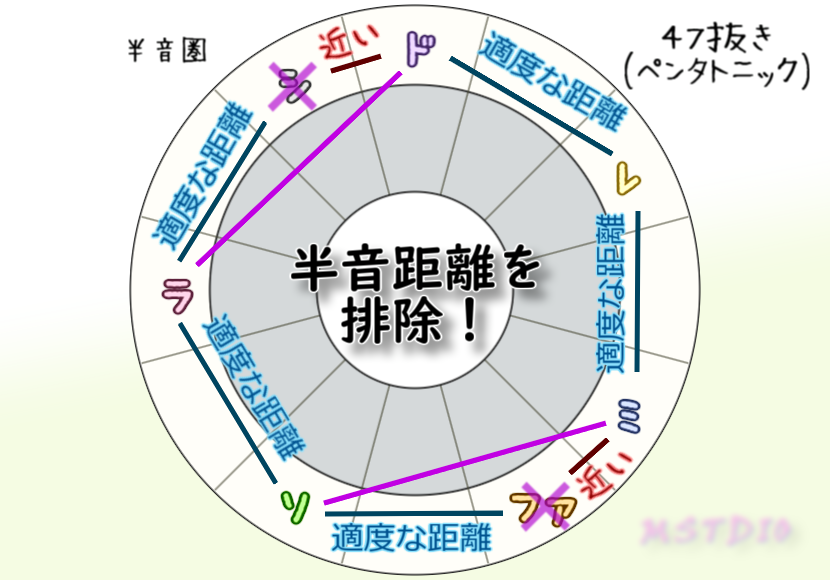
半音距離で音同士が離れればハーモニー的にいいっていうのであれば、ミとファやシとドの半音密着してるところは捨てちゃってもよさそうだよね。音を7つ以下にしちゃって。
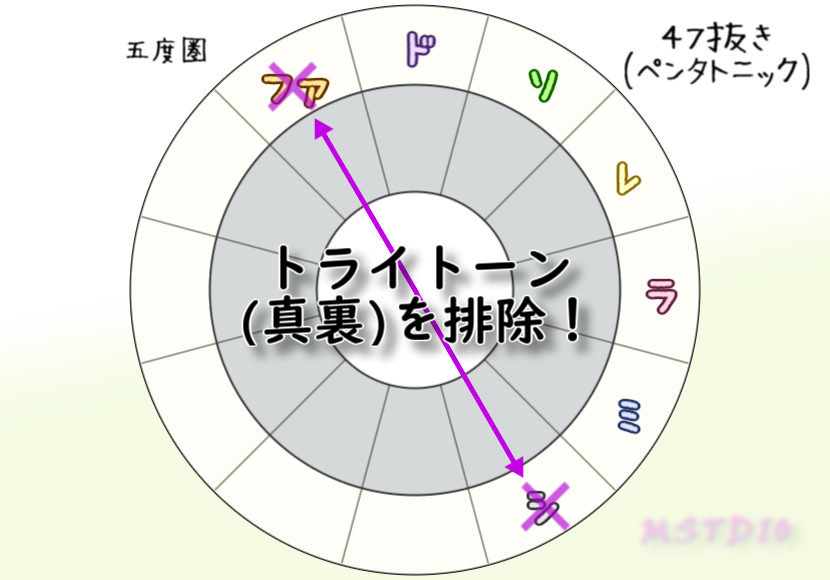
気づいた人もいるかもだけど、それってすなわち47抜き音階(ペンタトニックスケール)になるんだ。メロディック的(五度圏)には半音距離がない音階で、ハーモニック的(半音圏)にはトライトーンがない音階。ハーモニック的調和を考えると捨てるのは端っこのファやシだね。
ハーモニー的(和声的)にそれでもいいかもしれないけど、でもメロディ的(旋律的)にはラ⇔ドやミ⇔ソの間に半音3つ分の距離隙間が空いてしまうから、音高落差が生まれて滑らかさを欠如しちゃうね。
例えば「ソーラーシードー」ってメロディが「ソーラーラードー」になるって考えると、ドに向かう滑らかで穏やかなアプローチがなくなっちゃった感あるよね。
そう考えると7つの音で構成されるダイアトニックスケールって和声的にも旋律的にも凄くバランスの取れた音階じゃない?
それこそ
- コード達:ダイアトニックで調和!
- メロディ:ペンタトニックで濁らせず!
のような合わせ技は調和の塊だね。
3度堆積和音が好まれる理由
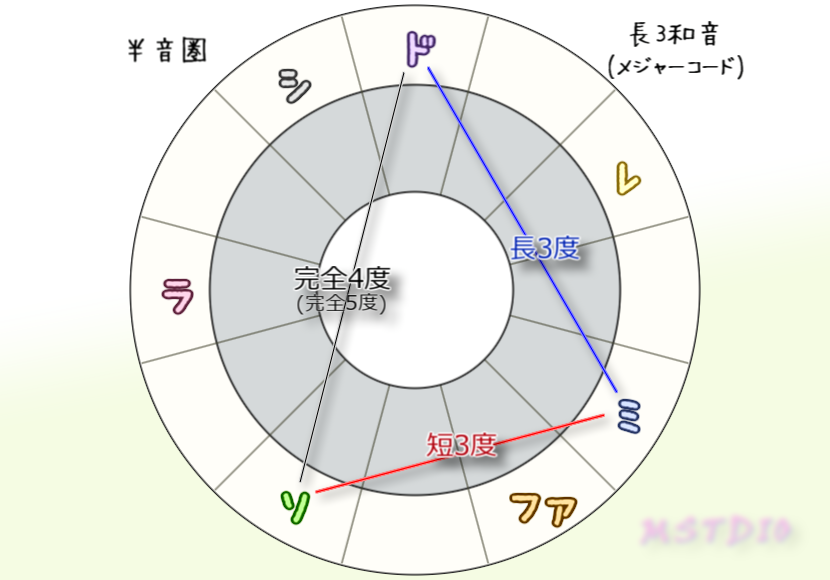
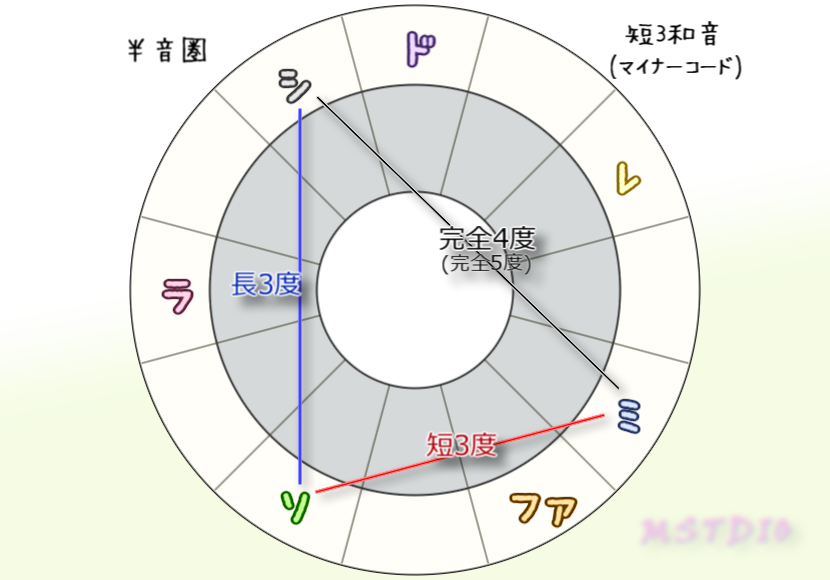
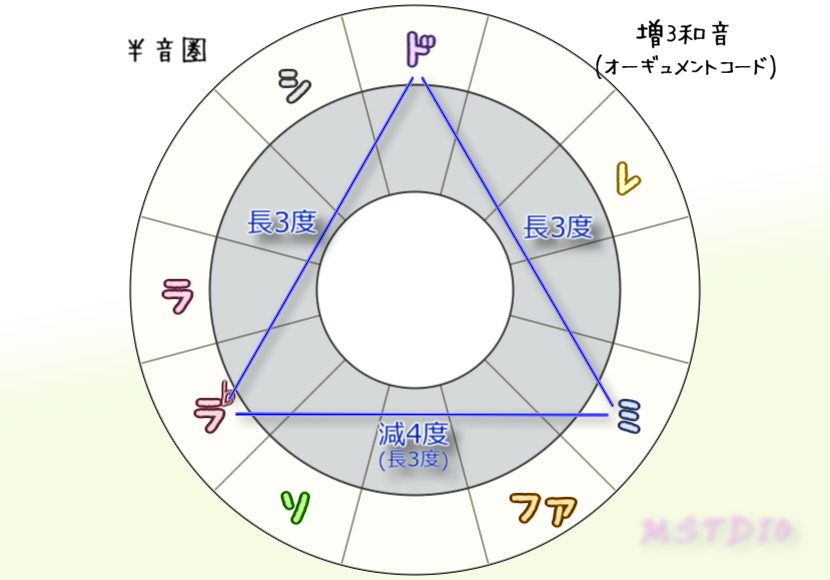
そして、なんで和音は3度堆積(ルート+3rd+5th)がしっくりくるのかってことも半音圏を見るとわかりやすい。なるだけ音が濁らないような3和音の選び方を考えてみる。3つの音が近すぎない選び方をすると、鋭角三角形(どの角も90度以下)になって、ドミソとかミソシとかのように3度ずつ積んだ形になる。だから3度堆積は調和を保ってるんだね。
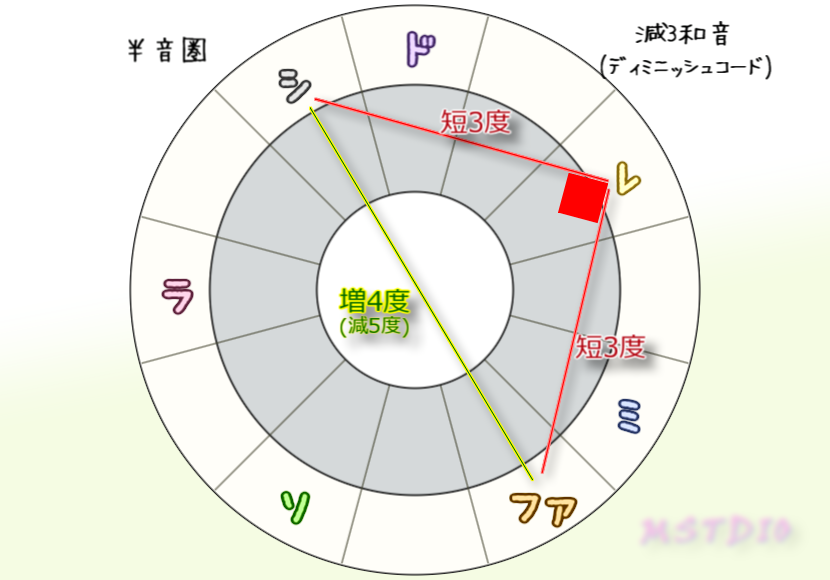
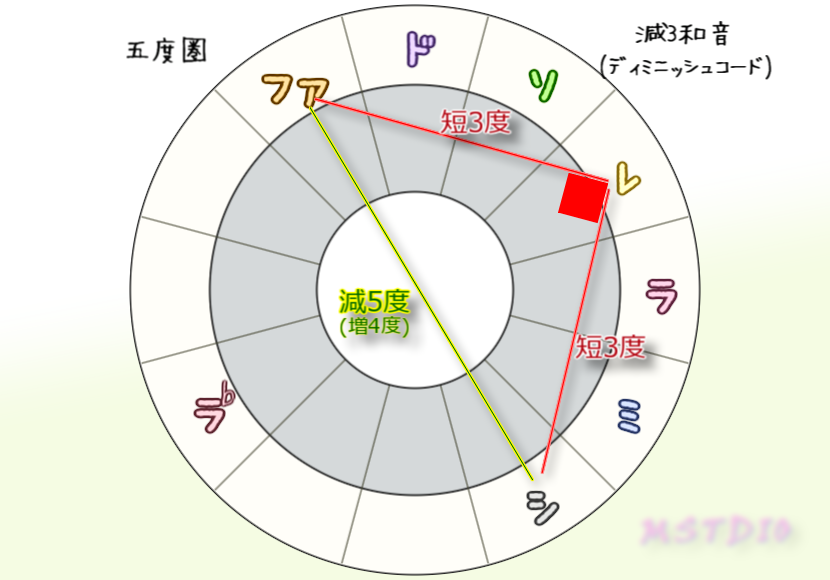
そしてシレファだけが中心点を通る直角二等辺三角形になる。そしてこれは五度圏上も全く同じ形で、中心点を通り悪魔の音程(=トライトーン)を持つ。濁るのも納得だね。
3点が遠い三角形=大きな三角形ほど濁らないってことは、正三角形は最強そうだよね。三角形ってどんなコードかっていうと、augコードになる。
例えばA♭aug=ラ♭ドミって不安定じゃない??その通り。実は蓋を開けてみると、これは五度圏上も正三角形になってしまうんだ。隣り合うほど調和するはずの五度圏上でも程よく離れた3音となってしまうので、和音が不安定なんだ。
ペンタトニックスケール
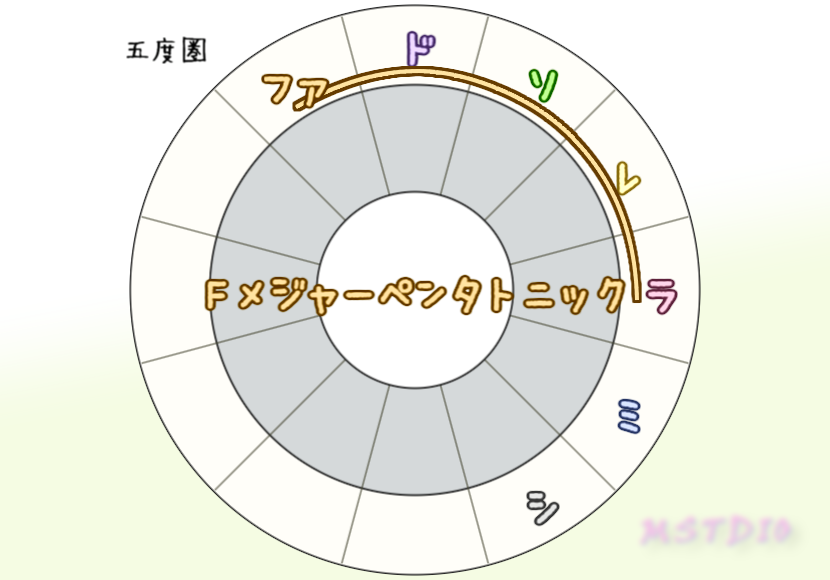
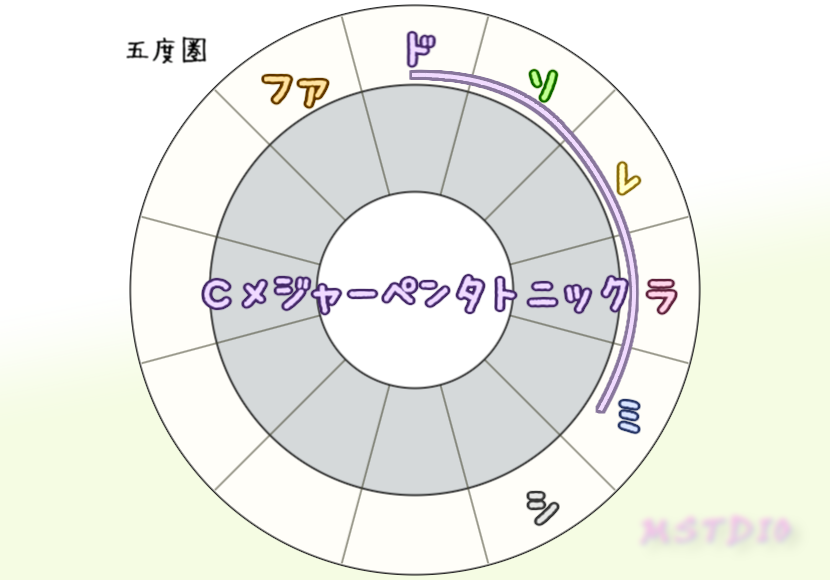
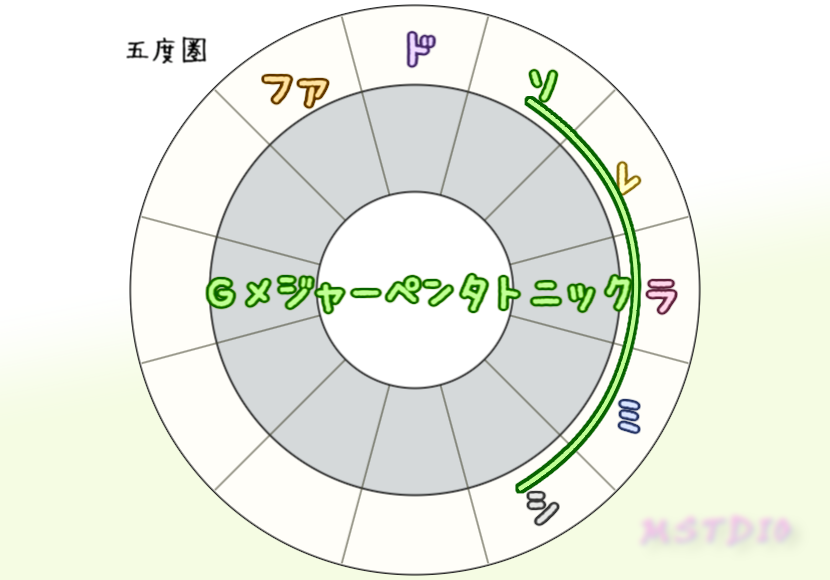
五度圏で隣り合う連続5音はペンタトニックスケール(ヨナ抜き音階)になるよ。基準の音は、ファ・ド・ソの3種類選べるから、裏を返すとCメジャーペンタトニック(ドレミソラ)はCメジャーキー以外にGメジャーキーやFメジャーキーにも存在する⇒これらの調と相性がいいスケールだってのがわかるね。
例えば、田中秀和氏の花ハ踊レヤいろはにほっていう作品(分析記事執筆中)では、冒頭とサビのメロディは同じメロディで、背景は別の調っていうギミックが使われてるよ。メロディがペンタトニックだから隣の調でも成立してるんだ。
ヨナ抜き音階は、メジャースケールの4、7番目を抜いた音階。これは五度圏上のメジャースケールの端っこの音(上のCメジャーペンタトニックの図のファとシ)だね。
属調・下属調との差異
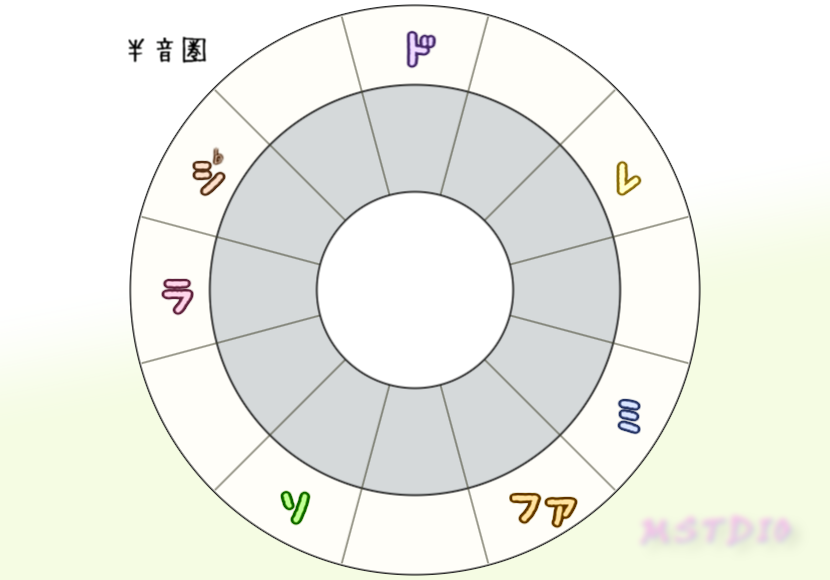
もう一つ面白いのは、半音圏で隣の音と隣接してる悪魔の音程のシとファは、あいてるマスに1つ動かしてもまたダイアトニックの形になるってこと。
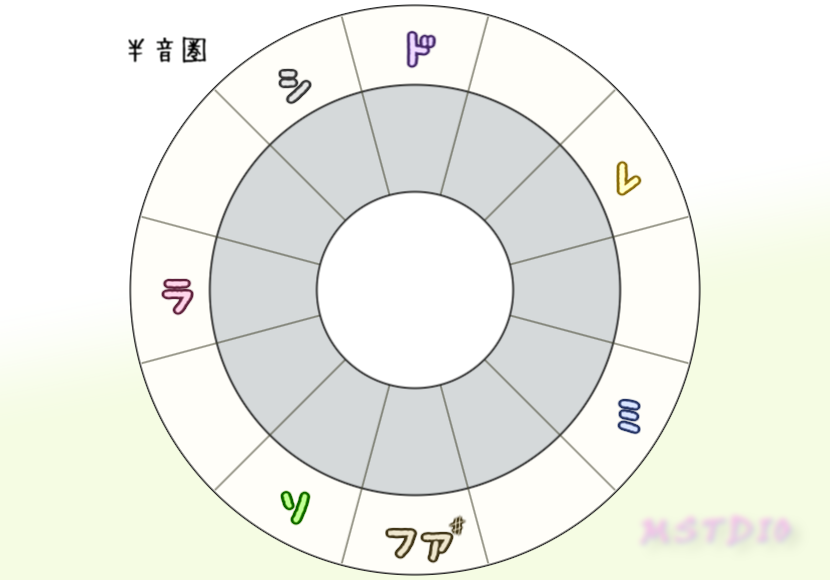
下の左図はダイアトニックであるFメジャースケール、半音隣合うシ♭をあいてる隣にずらすとまたダイアトニックの形のCメジャースケールになって、ファを右にずらすとまたダイアトニックの形のGメジャースケールになるってこと。
ダイアトニックの形になるということは、音を1つずらしただけで元の形を150度くらい回転させた形と同じ形になるってことなんだ。幾何的な調和を感じるね。
これはCメジャースケールからGメジャースケールやFメジャースケールの変化と同じだね(この先属調、下属調という名前で近さの記事を書くよ)
まとめ
とまぁ、五度圏/半音圏という距離の整理をスタートに思いつくままに音楽の神秘的な気づきを並べてきたけど、まとめるとこんな感じ!
- 音楽空間の距離の話
- 距離には半音距離と五度距離があってそれしかないって話
- 半音距離はメロディックな距離、旋律的距離
- 五度距離はハーモニックな距離、和声的距離
- 距離の可視化として半音圏と五度圏が役立ちそうって話
という前提の皮切り話と、これらから見る音楽の神秘的な気づきは
- ダイアトニックは和声的距離で密集してる、調和のとれたスケール
- ダイアトニックは旋律的にも調和のとれたスケール
- 3度堆積和音の半音圏上でのカタチ
- 3度堆積和音が好まれることの可視化
- ペンタトニックスケールが下属調、属調に馴染みやすいという可視化
- ダイアトニックスケールの幾何的な調和性
- 下属調、属調との近さの可視化
五度圏にまつわる話はここまでだよ!(多分)今後この距離の概念を用いて音楽に切り込んでいくよ!
それじゃーね!
読んでくれてありがとー! ↓ よければランキングや広告ポチもお願いします!

![]()
![]()




コメント
[…] ような効果がある。これは、直前までに聴いていた世界観(背景スケール)から逸脱する音が少ない(6番目の音1つだけ)であることや、コード構成音がaug(増三和音)を含むことが効いてるね。音楽的な和声的/旋律的距離の記事…ようにaugコードはトライアドの中でもっとも離れた位置関係の和音で不安定さを煽る。 […]